Welcome to the world of algorithm efficiency, where we explore "Big O Notation." If you've ever wondered how computer scientists measure algorithm performance or why some code runs faster than others, you're in the right place. In this blog post, we'll dive into the concept of Big O notation, breaking it down for both beginners and experienced programmers. Whether you're preparing for interviews, improving your code, or expanding your programming skills, understanding Big O is essential for unraveling how algorithms work. Let's begin this journey into algorithm analysis.
There is a way of learning DSA, so we will follow that:
Big O -> How to solve Problems -> Data structures -> algorithms.
means that I'll provide the link to the next topic at the end of the blog. so stay connected
Big O
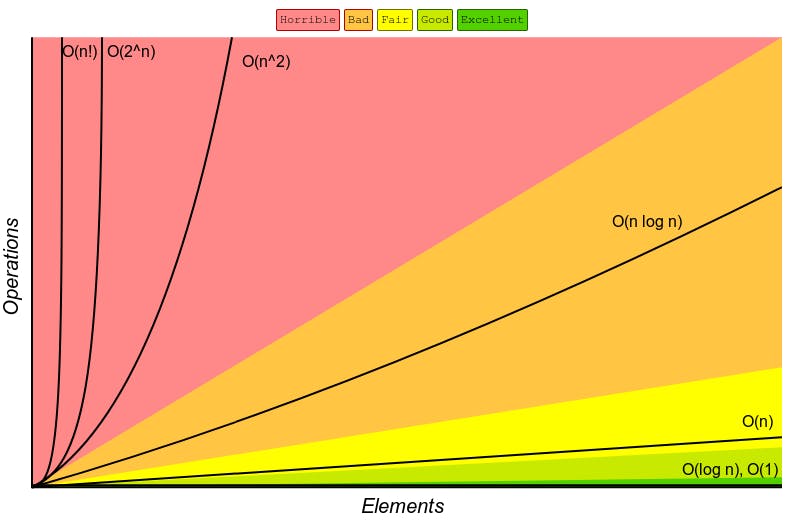
The official term Big O is also said as Big O asymptotic analysis.
Big O notation is the language we use to talk about how long an algorithm takes to run (often denoted as O ( )).
Space Complexity: Time is not the only thing that matters in an algorithm. we might also care about the memory and space required by an algorithm.
Space complexity is a parallel concept to time complexity. if we need to create an array of size n this will require O (n) space. if we need a two-dimensional array of size (n * n), this will require O(n^2) space.
Best, Average, and worst: Big O notation often describes the worst-case time complexity of an algorithm. However, you can also analyze the best and average cases to get a more complete picture of an algorithm's performance.
Comparing Algorithms: Big O notation is a valuable tool for comparing the efficiency of different algorithms for solving the same problem. it helps you choose the most appropriate algorithm for a specific task.
Big O notation is an upper bound: Remember that Big O notation describes an upper bound on the algorithm's complexity. it provides an asymptotic analysis, focusing on how the algorithm behaves as the input size becomes very large.
O(n) - Linear time: Linear time complexity (O(n)) means an algorithm's performance grows proportionally with the input size. if you double the input size, the algorithm roughly takes twice as long. It's often seen in the algorithms that iterate through input data once, performing a constant amount of work for each element. Examples include iterating through arrays of lists.
O (1) - Constant time: Constant time complexity O(1) means an algorithm's performance remains the same regardless of input size. it always takes the same amount of time to execute regardless of how large the input is. this is achieved by performing a fixed number of operations, usually without looping or iterating through the data. An example is accessing an an element in array by its index, which takes the same time regardless of the array's size.
O (n^2) - Quadratic time: Quadratic time complexity, denoted as O(n^2), describes an algorithm whose execution time grows quadratically with the input size. Imagine you have a nested loop where, for each element in a collection, you act with every other element. As the collection gets larger, the number of actions required doesn't increase linearly but rather exponentially. It's like if you had 10 items, you'd need to perform 100 actions; with 100 items, it would be 10,000 actions, and so on. Quadratic algorithms, such as the Bubble Sort, tend to be slow for large datasets, so they're not ideal for optimizing performance. Instead, it's often better to use algorithms with lower time complexities, like O(n log n) or O(n), for more efficient processing.
// log all the pairs of boxes
const boxes = ["a", "b", "c", "d", "e"];
function logAllPairsOfBoxes(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
console.log(array[i], array[j]);
}
}
}
logAllPairsOfBoxes(boxes);
// this shows the quadratic time complexity.. in the nested loop.
//Note : if we have three nested layers the time complexity will be O (n^3)
//but if you are having it .. it's horrible and you're something wierd.
- O (n!): This is the most horrible thing known as Factorial time complexity. As you work in the code you will not encounter this but still, I want to let you know that it exists. This Big O notation represents a factorial time complexity, indicating that an algorithm's runtime grows factorially with the input size 'n.' In simpler terms, it implies that the number of operations increases rapidly as 'n' grows. This means that you are looping over every input.
Rules for guidance and Principles of big O notation.
Now that we've grasped the fundamental concepts of Big O notation, let's delve deeper into the world of algorithm analysis. In the realm of efficient coding, it's not just about knowing what Big O represents; it's also about understanding the rules and principles that guide its application. These rules serve as our compass in evaluating algorithm performance and making informed choices. Today, we'll introduce you to four of these rules:
Worst case rule.
Drop the constant rule.
Different terms for inputs.
Drop non-dominants.
These rules are like the first steps on a journey into algorithmic optimization. Stay tuned because, in subsequent discussions, we'll unveil more valuable rules and insights, each adding a layer of understanding to help you unravel the complexities of algorithms and make your code more efficient.
As we progress further, we will explore these rules in tandem with our journey through Big O notation and other related concepts.
Worst case rule: The Big O worst-case rule is a way to describe the upper bound or maximum time or space complexity of an algorithm. it focuses on the scenario where the algorithm takes the most time or space to complete, ensuring that we have a pessimistic estimate of its efficiency as the input size grows. it helps in making safe assumptions about the algorithm's performance. even in the worst situations.
Drop the constants: The "Drop the constant" rule in Big O notation means that we disagreed with constant factors when analyzing algorithmic complexity. we focus on how complexity scales with input size rather than precise execution time. For example, O (2n) simplifies to O(n), as the constant factor (2) doesn't significantly impact the growth rate. the rule simplifies complexity analysis and emphasizes the most significant factors affecting the performance of an algorithm as input size increases.
function example1(arr) {
for (let i = 0; i < 3 * arr.length; i++) {
// Some operation
}
}
// O(3n) simplifies to O(n) by dropping the constant 3.
Different terms for input: Suppose you have an algorithm that processes two arrays, one with 'a' elements and the other with 'b' elements, and it performs some operation on each element of both arrays. The runtime complexity of this algorithm might be O(a + b), indicating that the time it takes to process both arrays grows linearly with the total number of elements in both arrays combined. If 'a' and 'b' are both very large, the algorithm's runtime will be relatively larger than when 'a' and 'b' are small.
In summary, O(a + b) is a notation used to describe the combined time complexity of an algorithm in terms of two input variables 'a' and 'b', indicating that the algorithm's runtime grows linearly with their sum, without distinguishing their impacts.
If they are nested means A and B arrays are nested then the time complexity will be O (A*B).
Drop the non-dominant term: Dropping non-dominant terms in Big O notation is a simplification technique used to focus on the most significant factor affecting an algorithm's time complexity. It means neglecting less influential terms or constants when describing an algorithm's growth rate concerning input size. Here's a concise explanation:
Big O Notation: In algorithm analysis, Big O notation (e.g., O(n), O(n^2)) describes an upper bound on an algorithm's time complexity as the input size (n) grows.
Dominant Term: The dominant term is the part of the algorithm that has the most significant impact on its runtime as the input size increases.
Non-Dominant Terms: Non-dominant terms include less influential factors, often constants or lower-order terms, that have a negligible effect on runtime as the input size grows.
Example 1 (Dropping Constants):
- O(3n^2) simplifies to O(n^2) by dropping the constant 3 because it doesn't affect the growth rate significantly.
Example 2 (Dropping Lower-Order Terms):
- O(n^2 + 5n + 1) simplifies to O(n^2) by dropping the lower-order terms 5n and 1 since n^2 dominates their growth.
Focus on Dominant Terms: The purpose is to focus on the dominant term, which provides a clear understanding of how the algorithm scales with input size.
Simplification for Clarity: Dropping non-dominant terms simplifies analysis, making it easier to compare and choose algorithms based on their fundamental growth rates.
Code Example (Dropping Constants):
function example1(arr) { for (let i = 0; i < 3 * arr.length; i++) { // Some operation } } // O(3n) simplifies to O(n) by dropping the constant 3.Code Example (Dropping Lower-Order Terms):
function example2(arr) { for (let i = 0; i < arr.length * arr.length + 5 * arr.length + 1; i++) { // Some operation } } // O(n^2 + 5n + 1) simplifies to O(n^2) by dropping the lower-order terms 5n and 1.
In summary, dropping non-dominant terms in Big O notation is a simplification technique that helps focus on the primary factor influencing an algorithm's time complexity, making it easier to compare and understand algorithm efficiency.
Space Complexity
Space complexity refers to the amount of memory or storage space required by an algorithm or program to execute and solve a problem, as a function of the input size. It focuses on understanding how much additional memory is needed beyond the input data itself.
When analyzing space complexity, we consider various factors, such as the size of data structures, temporary variables, and the call stack used during the program's execution. A program with low space complexity uses minimal memory relative to the input size, while a high space complexity may require a substantial amount of memory, potentially leading to issues like inefficient memory usage or even program crashes when dealing with large datasets.
Efficient space complexity is vital in optimizing program performance and ensuring that applications can handle memory constraints gracefully. By managing space effectively, developers can design programs that not only work efficiently but also scale well to accommodate growing data requirements while minimizing memory usage.
Pillars of Programming
The three pillars of programming—readability, memory efficiency, and speed—are crucial for writing high-quality code. Each pillar serves a distinct purpose in software development:
Readability:
Importance: Readable code is essential for collaboration, maintenance, and understanding. Code is often read more frequently than it is written.
Characteristics: Readable code is well-organized, well-documented, and follows consistent naming and coding conventions.
Benefits: It enhances code maintainability, reduces debugging time, and makes it easier for others (including your future self) to understand and modify the code.
Memory Efficiency:
Importance: Efficient memory usage is vital, especially in resource-constrained environments and when dealing with large datasets.
Characteristics: Memory-efficient code minimizes the use of memory resources, avoids memory leaks, and optimizes data structures for space.
Benefits: It prevents crashes and slowdowns due to excessive memory consumption, allowing your application to run smoothly even in memory-restricted scenarios.
Speed (Execution Efficiency):
Importance: Speed refers to how quickly your code performs tasks. Faster code is crucial for real-time applications, large-scale data processing, and responsive user experiences.
Characteristics: Speed-optimized code minimizes redundant operations, uses efficient algorithms, and optimizes critical code paths.
Benefits: Faster code results in improved user experiences, reduced latency, and more efficient resource utilization.
Now, to address your question about which code is "best" in terms of these pillars, it's important to recognize that there's often a trade-off among them. The "best" code depends on the specific context and priorities of your project:
Balancing All Three: The ideal code strikes a balance among the pillars, achieving reasonable readability, memory efficiency, and speed. Striving for all three is often a good goal in software development.
Context Matters: Depending on your project's context, one pillar may take precedence over the others. For example, in embedded systems, memory efficiency is critical, while in a user-facing web application, speed and readability may be more important.
Optimizing Where Necessary: In performance-critical parts of your code, such as inner loops, optimizing for speed and memory efficiency may be necessary, even if it slightly sacrifices readability. However, you should thoroughly document and comment on such sections to aid understanding.
Code Reviews: Regular code reviews with team members can help ensure that code is readable and maintainable while also addressing performance and memory issues.
Profiling: Use profiling tools to identify bottlenecks in your code. This allows you to focus optimization efforts where they have the most impact on speed and memory usage.
In summary, the "best" code prioritizes all three pillars but may emphasize one over the others based on context. Strive for a balance, optimize where necessary, and rely on collaboration, documentation, and profiling to make informed decisions about your code's quality.
Keep coding and exploring the world of algorithms! May your code always be efficient, readable, and lightning-fast. Happy coding!
Thanks for reading..
Stay Connected for all the blogs related to DSA .. i'll share the link to interconnect each topic step by step . thanks for all your love and please subscribe to my newsletter below to stay updated for my blogs ..
